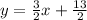Question

Consider the line y=-2/3x-4 Find the equation of the line that is perpendicular to this line and passes through the point (-3,2)

Answer 1

`y = (3)/(2)x + (13)/(2)`

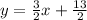
Explanation:

Perpendicular lines have negative reciprocals slopes, in which the product of their slopes result in -1.

Since the slope of the given line is m1 = -2/3, its negative reciprocal must be m2 = 3/2:

`m_(1) *m_(2) = (-(2)/(3)) ((3)/(2)) = -1`

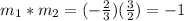
Next, we'll use the slope of the other line, m = 3/2, and the given point, (-3, 2) to solve for the y-intercept of the other line by substituting the values into the slope-intercept form:

y = mx + b

`2 = (3)/(2)(-3) + b`

`2 = -(9)/(2) + b`

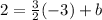
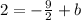
Add 9/2 to both sides to isolate b:

`2 + (9)/(2) = -(9)/(2) + (9)/(2)+ b`

`(13)/(2) = b`

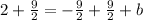
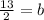
Therefore, the equation of the line perpendicular to
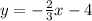`y = -(2)/(3)x - 4` is:

`y = (3)/(2)x + (13)/(2)`