Question

PLEASE HELP ITS DUE SOON! I DONT GET ANY OF THIS! HELP WOULD BE MUCH APPRECIATED! NEED THIS DONE BEEN STUCK ON THIS FOR WAY TO LONG!

YOU WILL GET 100 POINTS IF YOU HELP! QUESTION DOWN BELOW!!!!!
THIS IS MY LAST QUESTION!!

Answer 1

See below.

Explanation:

Vertical Angles Theorem

When two straight lines intersect, the opposite vertical angles are congruent.

Alternate Interior Angles Theorem

If a line intersects a set of parallel lines in the same plane at two distinct points, the alternate interior angles that are formed are congruent.

Transitive Property of Equality

If a=b and c=b, then a=c.

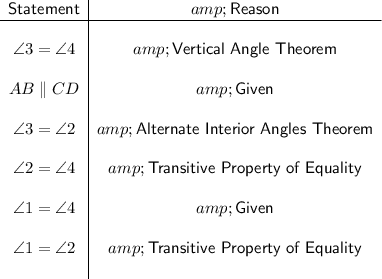
Proof that ∠1=∠2

• ∠3 is equal to ∠4 (Vertical Angle Theorem).
• As BC intersects the set of parallel lines AB and CD (given), ∠3 is equal to ∠2 (Alternate Interior Angles Theorem).
• If ∠3=∠4 and ∠3=∠2 then ∠2=∠4 (Transitive Property of Equality).
• Given that ∠1=∠4 and ∠2=∠4 then ∠1=∠2 (Transitive Property of Equality).

`\begin{array}c\sf Statement & \sf Reason\\\cline{1-2}\\ \angle 3 = \angle 4 & \textsf{Vertical Angle Theorem}\\\\AB \parallel CD & \textsf{Given}\\\\\angle 3 = \angle 2 & \textsf{Alternate Interior Angles Theorem}\\\\\angle 2 = \angle 4 & \textsf{Transitive Property of Equality}\\\\\angle 1 = \angle 4 & \textsf{Given}\\\\\angle 1 = \angle 2 & \textsf{Transitive Property of Equality}\\\\\end{array}`