Question

alpha writes the infinite arithmetic sequence \[10, 8, 6, 4, 2, 0 ,\ldots.\]beta writes the infinite geometric sequence \[9, 6, 4, \frac{8}{3}, \frac{16}{9}, \ldots.\]gamma makes a sequence whose $n^{\text{th}}$ term is the product of the $n^{\text{th}}$ term of alpha's sequence and the $n^{\text{th}}$ term of beta's sequence: \[10\cdot 9 \quad,\quad 8\cdot 6\quad ,\quad 6\cdot 4\quad,\quad 4\cdot \frac83\quad,\quad 2\cdot \frac{16}{9}\quad,\quad \ldots.\]what is the sum of gamma's entire sequence?

Answer 1

Consecutive terms in the α sequence have a common difference of

8 - 10 = 6 - 8 = 4 - 6 = … = -2

so they are given recursively by

`\begin{cases} \alpha_1 = 10 \\ \alpha_n = \alpha_(n-1) - 2 & \text{for } n\ge2 \end{cases}`

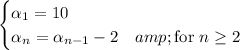
By substitution, we have

`\alpha_n = \alpha_(n-1) - 2 \\\\ \alpha_n = \alpha_(n-2) - 2\cdot2 \\\\ \alpha_n = \alpha_(n-3) - 3\cdot2 \\\\ \vdots \\\\ \alpha_n = \alpha_(n-(n-1)) - (n-1)\cdot 2 = \alpha_1 - 2(n-1) = 12-2n`

Consecutive terms in the β sequence have a common ratio of

6/9 = 4/6 = (8/3)/4 = … = 2/3

so the recurrence for these terms is

`\begin{cases} \beta_1 = 9 \\\\ \beta_n = \frac23 \beta_(n-1) & \text{for } n\ge2 \end{cases}`

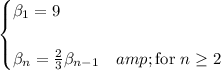
We can solve for
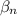`\beta_n` similarly:

`\beta_n = \frac23 \beta_(n-1) \\\\ \beta_n = \left(\frac23\right)^2 \beta_(n-2) \\\\ \beta_n = \left(\frac23\right)^3 \beta_(n-3) \\\\ \vdots \\\\ \beta_n = \left(\frac23\right)^(n-1) \beta_(n-(n-1)) = \left(\frac23\right)^(n-1) \beta_1 = (2^(n-1))/(3^(n-1)) \cdot 3^2 = (2^(n-1))/(3^(n-3))`

The γ sequence has
`n`-th term

`\gamma_n = \alpha_n \beta_n = (12-2n) (2^(n-1))/(3^(n-3)) = (108-18n) \left(\frac23\right)^(n-1)`

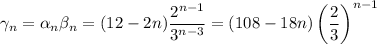
and we want to compute

`\displaystyle \sum_(n=1)^\infty \gamma_n = 108 \sum_(n=1)^\infty \left(\frac23\right)^(n-1) - 18 \sum_(n=1)^\infty n \left(\frac23\right)^(n-1)`

Recall the sum of an infinite geometric series with common ratio
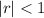`|r|<1` converges to

`\displaystyle \sum_(n=1)^\infty r^(n-1) = \frac1{1-r}`

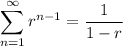
so that

`\displaystyle \sum_(n=1)^\infty \left(\frac23\right)^(n-1) = \frac1{1-\frac23} = 3`

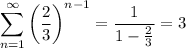
For the remaining sum, we can use the method shown in question [24494877] to compute

`\displaystyle \sum_(n=1)^\infty nr^(n-1) = \frac1{(1-r)^2}`

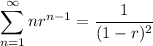
which gives

`\displaystyle \sum_(n=1)^\infty n \left(\frac23\right)^(n-1) = \frac1{\left(1-\frac23\right)^2} = 9`

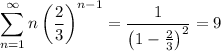
Then the infinite sum of the terms of γ converges to

`\displaystyle \sum_(n=1)^\infty \gamma_n = 108 \cdot 3 - 18 \cdot 9 = \boxed{162}`