Answer:
x ≥ 2
Explanation:
Given inequality:

Values of x less than 2
Substitute two values where x < 2 into the inequality:
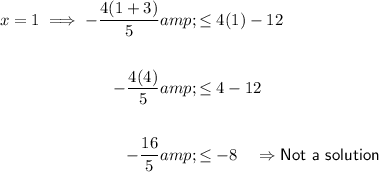
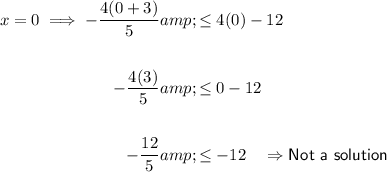
The values of x < 2 are not solutions to the inequality.
--------------------------------------------------------------------------------
Substitute the value of x = 2 into the inequality:
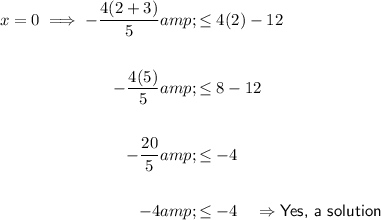
The value of x = 2 is a solution to the inequality.
--------------------------------------------------------------------------------
Values of x more than 2
Substitute two values where x > 2 into the inequality:
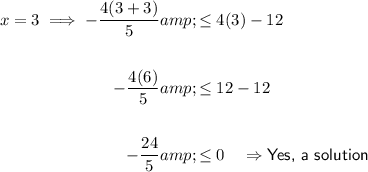
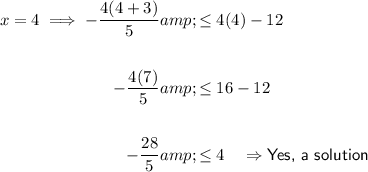
The values of x > 2 are solutions to the inequality.
--------------------------------------------------------------------------------
Therefore, the solution to the inequality appears to be x ≥ 2.
To check, solve the inequality:
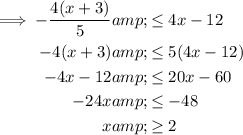
When graphing inequalities on a number line:
- < or > : open circle.
- ≤ or ≥ : closed circle.
- < or ≤ : shade to the left of the circle.
- > or ≥ : shade to the right of the circle.
To graph the solution to the inequality on number line, place a closed circle at x = 2 and shade to the right. (See attachment).