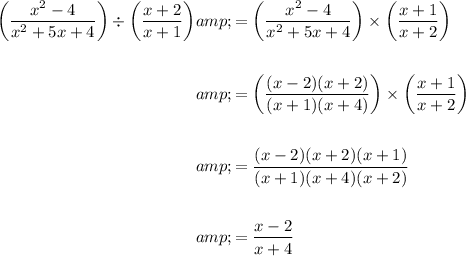Answer:
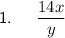
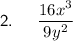

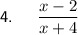
Explanation:
When dividing two fractions, multiply the first fraction by the reciprocal of the second fraction.
The reciprocal of a fraction is its inverse (swap the numerator and denominator).
Question 1

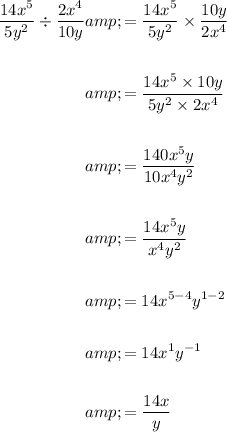
------------------------------------------------------------------------------------------
Question 2
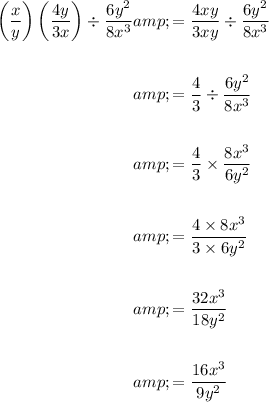
------------------------------------------------------------------------------------------
Question 3
![\begin{aligned}\left[(5(y+6))/(2(xy-3)) \right] / \left((y+6)/(4(xy-3))\right) & = \left[(5(y+6))/(2(xy-3)) \right] * \left((4(xy-3))/(y+6)\right)\\\\& = (5(y+6) * 4(xy-3))/(2(xy-3) * (y+6))\\\\& = (20(y+6)(xy-3))/(2(xy-3)(y+6))\\\\& = (20)/(2)\\\\&=10\end{aligned}](https://img.qammunity.org/2023/formulas/mathematics/high-school/ohqvzegyo8p6h471ox3i8idph4wb3ngv86.png)
------------------------------------------------------------------------------------------
Question 4
Factor the numerator and denominator of the first fraction.
Apply the Difference of Two Squares to the numerator:
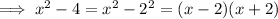
Factor the denominator:
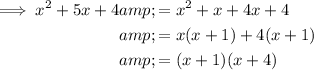
Therefore: