Question

The Picture Has The Question.

Answer 1

Angle RQS measures 104°, and angle TQS measures 76°.

Step-by-step explanation:

`14x + 6 + 10x + 6 = 180`

`24 + 12 = 180`

`24x = 168`

`x = 7`

Angle RQS measures:

14(7) + 6 = 98 + 6 = 104 degrees

Angle TQS measures:

10(7) + 6 = 70 + 6 = 76 degrees

Answer 2

∠RQS = 104°

∠TQS = 76°

Step-by-step explanation:

A linear pair consists of two adjacent angles whose measures sum to 180°. In other words, these are two angles that, when combined, form a straight line.

Therefore, to find the measures of ∠RQS and ∠TQS, set the sum of the two angle expressions equal to 180°, solve for the variable x, then substitute x back into the angle expressions.

Find the value of x:

`\begin{aligned}\angle RQS+\angle TQS&=180^(\circ)\\(14x+6)^(\circ) +(10x+6)^(\circ)&=180^(\circ)\\14x+6+10x+6&=180\\24x+12&=180\\24x+12-12&=180-12\\24x&=168\\24x / 24&=168 / 24\\x&=7\end{aligned}`

Now, substitute the found value of x into the expressions for each angle:

`\begin{aligned}\angle RQS&=(14x+6)^(\circ)\\&=(14(7)+6)^(\circ)\\&=(98+6)^(\circ)\\&=104^(\circ)\end{aligned}`

`\begin{aligned}\angle TQS&=(10x+6)^(\circ)\\&=(10(7)+6)^(\circ)\\&=(70+6)^(\circ)\\&=76^(\circ)\end{aligned}`

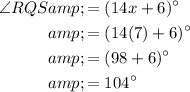
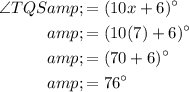
Therefore, the measures of ∠RQS and ∠TQS are:

• ∠RQS = 104°
• ∠TQS = 76°