Answer:
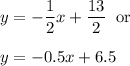
Explanation:
The slope-intercept form of a straight line is
y = mx + b
where m = slope and b = y-intercept
A line perpendicular to the above line will have a slope = -1/m and an intercept b which has to be determined depending on a point the line passes through
Given
Line 1: y = 2x - 6
Slope m = 2
Line 2 perpendicular to Line 1 will have slope = -1/2 = -0.5
So the equation would be y = (-1/2)x + b
We can solve for b given the info that the line passes through (5,4)
Substitute x = 5 and y = 4 in line 2 equation:
4 = (-1/2)5 + b
4 = -5/2 + b
4 + 5/2 = b
8/2 + 5/2 = b
13/2 = b
or b = 13/2
So equation of line perpendicular to 2x -6 is
y = (-1/2)x + 13/2
or
y = -0.5x + 6.5