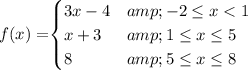Answer:
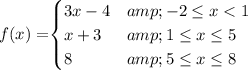
Explanation:
The permissible values of x for a function is called the domain of the function. Permissible values mean that the function is real and defined.
The range of a function is the set of all y values for the domain
If a point on a graph is a filled circle, that point is included in the domain(x-value) and represents a ≤ or a ≥ inequality
If a point on a graph is an unfilled or hollow circle, that point is not included in the domain(x-value) and represents a < or a >inequality
Let's look at the three parts of the given piecewise graph
Piecewise part A
We see that the minimum and maximum values of x for this function are x = -2 and x = 1 respectively. The point corresponding to x= 1 is a hollow circle so it is not included in the domain whereas the point corresponding to x = -2 is included
Let's find the equation of this line:
Take 2 points on the line. We choose points (0, -4) and (1, -1)
Slope of this line is -1 -(-4)/(1-0) = (-1 + 4)/1 = 3
The y-intercept is -4
So equation of the line is y = 3x -4 for -2 ≤ x < 1
Proceeding in a similar manner we can determine the domain and function equation for the other two pieces, B and C
Piecewise part B
Domain of x : 1 ≤ x ≤5
Slope = (8-4)/(5-1) = 4/4 = 1
Equation is of the form y = 1x + b
To calculate b, plug in values of x = 1, y = 4 to get
4 = 1(1) + b
b = 3
Equation of this piecewise function is
y = x + 3 for 1 ≤ x ≤ 5
Piecewise Part C
This is a flat horizontal line at y = 8
So that is the equation of the line
The domain of this piece is 5 ≤ x ≤ 8
So we get y = 8 for
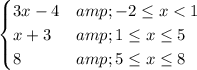
Normally, instead of using y we use f(x)
Putting all this together we get the piecewise function defined as