Question

What are m ∠DBC, m ∠ABD, and m ∠ABC

Answer 1

`\\ \sf\longmapsto 2x+1+4x+19=8x-10`

`\\ \sf\longmapsto 6x+20=8x-10`

`\\ \sf\longmapsto 8x-6x=20+10`

`\\ \sf\longmapsto 2x=30`

`\\ \sf\longmapsto x=15`

Now

• <DBC=4(15)+19=60+19=79
• <ABD=2(15)+1=30+1=31
• <ABC=79+31=110

Answer 2

Hello inquins!

`\huge \boxed{\mathbb{QUESTION} \downarrow}`

What are m ∠DBC, m ∠ABD, and m ∠ABC.

`\large \boxed{\mathfrak{Answer \: with \: Explanation} \downarrow}`

We can see from the figure that,

∠ABC = ∠ABD + ∠DBC ------- eq. (1)

The values of the angles are given as :-

• ∠ABC = 8x - 10
• ∠ABD = 2x + 1
• ∠DBC = 4x + 19

Now, let's substitute these values in eq. (1) & solve it.

∠ABC = ∠ABD + ∠DBC

`\tt \: 8x - 10 =( 2x + 1) +( 4x + 19) \\ \tt 8x - 10 = 2x + 1 + 4x + 19 \\ \tt 8x - 10 = 2x + 4x + 1 + 19 \\ \tt 8x - 10 = 6x + 20 \\ \tt 8x - 6x = 20 + 10 \\ \tt \: 2x = 30 \\ \tt \: x = (30)/(2) \\ \underline{\underline{ \bf \: x = 15}}`

• The value of x is 15.

__________________

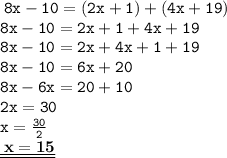
Now, let's find the measure of the angles.

1. m ∠ABC = 8x - 10 = 8(15) - 10 = 110°.
2. m ∠ABD = 2x + 1 = 2(15) + 1 = 31°.
3. m ∠DBC = 4x + 19 = 4(15) + 19 = 79°.

__________________

Hope it'll help you!

ℓu¢αzz ッ