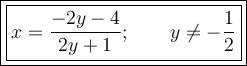Answer:
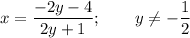
Explanation:
Given equation:
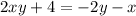
To solve for the given equation for x, we need to rearrange the equation to isolate x.
Begin by adding x to both sides of the equation:
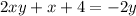
Now, subtract 4 from both sides:
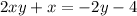
Factor out x from the left side of the equation:
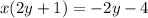
Finally, divide both sides of the equation by (2y + 1):
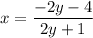
In a rational equation, if the denominator is equal to zero, the equation is undefined. In this case, the denominator is equal to zero when y = -¹/₂, therefore: