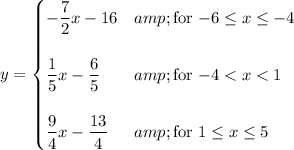Question

PLEASE PLEASE PLEASE!!!!!!!!!!HELP HELP HELP HELP HELP HELP!!!! IM CRYING IM STUCK

Answer 1

`y=\begin{cases}-(7)/(2)x-16&\text{for $-6\le x\le-4$}\\\\(1)/(5)x-(6)/(5)&\text{for $-4 < x < 1$}\\\\(9)/(4)x-(13)/(4)&\text{for $1\le x\le 5$}}\end{cases}`

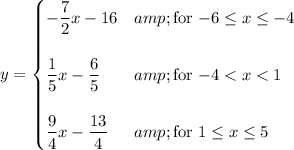
Explanation:

You want the piecewise function that describes the relation shown in the graph.

Relation

The relation shown consists of three line segments connecting the points ...

(-6, 5) and (-4, -2)

(-4, -2) and (1, -1)

(1, -1) and (5, 8)

Lines

The equations for the lines between the pairs of points can be written using the slope formula and the point-slope equation of a line.

The slope formula tells you the slope is ...

m = (y2 -y1)/(x2 -x1)

And the point-slope equation of a line is ...

y -y1 = m(x -x1)

If we add y1 to the equation of the line, and substitute the equation for m, we get ...

y = (y2 -y1)/(x2 -x1)(x -x1) +y1 . . . . . . a 2-point formula for a line

Application

Between x-values -6 and -4, the equation of the line will use the first pair of points:

y = (-2 -5)/(-4 -(-6))(x -(-6)) +5

y = -7/2(x +6) +5 = -7/2x -16

Between x-values -4 and 1, the equation of the line will use the second pair of points:

y = (-1-(-2))/(1 -(-4))(x -(-4)) +(-2)

y = 1/5(x +4) -2 = 1/5x -6/5

Between x-values 1 and 5, the equation of the line will use the last pair of points:

y = (8 -(-1))/(5 -1)(x -1) +(-1)

y = 9/4(x -1) -1 = 9/4x -13/4

Piecewise function

The piecewise function uses the equation for the line that is applicable for the appropriate x-values. We have listed those sets of x-values above.

We need to make sure that the function has only one definition for any given value of x. When two segments have a point in common, we need to make sure only one segment includes it.

`y=\begin{cases}-(7)/(2)x-16&\text{for $-6\le x\le-4$}\\\\(1)/(5)x-(6)/(5)&\text{for $-4 < x < 1$}\\\\(9)/(4)x-(13)/(4)&\text{for $1\le x\le 5$}}\end{cases}`