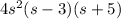Question

Completely factor 4s4 +8s3 - 60s².

O 45² (s - 5)(s + 3)
O This polynomial does not factor.
4s² (s 15)(s + 4)
4s² (s + 5)(s − 3) ​

Answer 1

4s² (s + 5)(s − 3) ​

Explanation:

Factor
`4s^(4) +8s^(3)-60s^(2)`

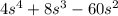
45² (s - 5)(s + 3)

This polynomial does not factor.

4s² (s 15)(s + 4)

4s² (s + 5)(s − 3) ​

The common term is
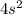`4s^(2)` so:

`4s^(2) (s^(2) +2s-15)`

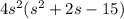
assume:

a = 1

b = 2

c = -15

Find two numbers that sum to 2 and multiply to -15:

-3+5 = 2

-3 × 5 = -15

so
`(s^(2) +2s-15) = (s-3)(s+5)`

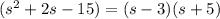
Plug in to
`4s^(2) (s^(2) +2s-15)`

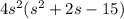
to get:
`4s^(2) (s-3)(s+5)`