The PDF for the wait time (denoted by the random variable X) is

where λ = 1/75. We want to find Pr[X > 70 | X ≥ 40]. Pierre has already been waiting for 40 min, so if he waits another 30 min he will have waited for a total of 70 min.
By definition of conditional probability,
Pr[X > 70 | X ≥ 40] = Pr[X > 70 and X ≥ 40] / Pr[X ≥ 40]
If X > 70, then automatically X ≥ 40 is satisified, so the right side reduces to
Pr[X > 70 | X ≥ 40] = Pr[X > 70] / Pr[X ≥ 40]
Use the PDF or CDF to find the remaining probabilities. For instance, using the PDF,
![\mathrm{Pr}[X > 70] = \displaystyle \int_(-\infty)^(70) f_X(x) \, dx = \int_0^(70) f_X(x) \, dx \approx 0.3932](https://img.qammunity.org/2023/formulas/mathematics/college/slnkf7fw4gra0m9aiqzp79mdba5cnaxnt1.png)
Or, using the CDF,
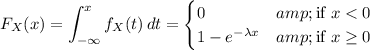
![\implies \mathrm{Pr}[X > 70] = 1 - \mathrm{Pr}[X \le 70] = 1 - F_X(70) \approx 0.3932](https://img.qammunity.org/2023/formulas/mathematics/college/gfkgdlutwtxt09qunypbos8v6r6b84363w.png)
Similarly, you'll find that Pr[X ≥ 40] ≈ 0.5866.
It follows that
Pr[X > 70 | X ≥ 40] ≈ 0.3932 / 0.5866 ≈ 0.6703