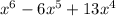Explanation:
Let use the following rules to construct a polynomial,
Rule 1:
If r is a zero of some polynomial, f(x), then

is a factor of the polynomial
We first know that one of our zeroes are real, which is 0.
So since r=0
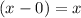
is a factor
However, since the root ,0, has a multiplicty of 4, that basically means we have 0 as a root 4 times or basically we multiply the factor 4 times.
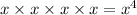
This leads to an another rule:
If a polynomial has a zero, r that has a multiplicty of k,
we represent the factor as
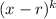
where k is all integers greater than 0.
So to reinforce myself, since 0 has a multiplicty of 4, we have
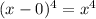
So our first factor is
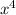
Part 2: Complex Zeroes.
When dealing with complex zeroes, we must note this rule.
if (a+bi) is a zero of some polynomial, p then its conjugate (a-bi) is a factor as well.
So if 3-2i is a factor, then
3+2i is a factor as well.
Using Rule 1, our factors now become
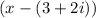
and
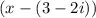
So our factors are
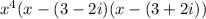
To simplify use FOIL Method,
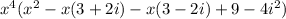

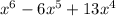
So our polynomial is