Answer:
See attachment.
Explanation:
Given absolute value function:
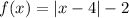
The parent absolute value function is f(x) = |x|.
Graph of the parent absolute value function:
- Vertex at (0, 0)
- |y| = -x if x ≤ 0
- |y| = x if x ≥ 0
Translations
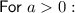
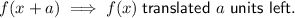

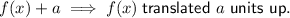

The graph of the given function is a transformation of the parent function by:
- Translation of 4 units right.
- Translation of 2 units down.
Therefore, the vertex of the given function is (4, -2).
Find two further points on the graph by inputting x-values either side of the x-value of the vertex into the given function:
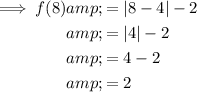
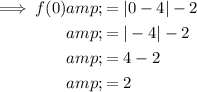
To draw the graph of the given function:
- Plot the vertex (4, -2).
- Draw a straight line from the vertex through point (8, 2).
- Draw a straight line from the vertex through point (0, 2).