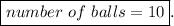Question

what is the maximum number of balls of clay of radius 2 that can completely fit inside a cube of side length 7 assuming the balls can be reshaped but not compressed before they are packed in the cube?

Answer 1

Number of balls of clay: 10

Explanation:

The volume of the cube is
`$V_{\text{cube}}=7^3=343,$`

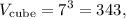
and the volume of a clay ball is:
`$V_{\text{ball}}=\frac43\cdot\pi\cdot2^3=(32)/(3)\pi.$`

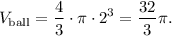
Since the balls can be reshaped but not compressed, the maximum number of balls that can completely fit inside a cube is

`\[\left\lfloor\frac{V_{\text{cube}}}{V_{\text{ball}}}\right\rfloor=\left\lfloor(343)/((32\pi)/(3) )\right\rfloor.\]`

Approximating with
`$\pi\approx3.14`

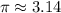
We have:

`\[\left\lfloor\frac{V_{\text{cube}}}{V_{\text{ball}}}\right\rfloor=10.23565228`

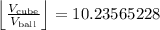
We simplify to get:

`\[\left\lfloor\frac{V_{\text{cube}}}{V_{\text{ball}}}\right\rfloor\approx10`

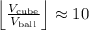
So:

`\boxed{number\ of\ balls = 10}.$`