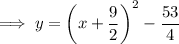Answer:
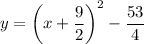
Explanation:
Vertex form of a quadratic equation:
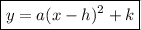
where:
- (h, k) is the vertex.
- a is the leading coefficient.
To find the vertex form of a quadratic equation, complete the square.
Given quadratic equation:
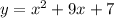
Add and subtract the square of half the coefficient of the term in x to the right side of the equation:
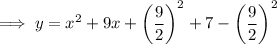
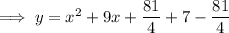
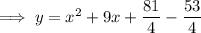
Factor the perfect square trinomial formed by the first 3 terms: