Question

I have one fair 6-sided die and one unfair 6-sided die. On the unfair die, the probabilities of rolling numbers 2,…,6 are equal and the probability of rolling a 1 has a different value. I roll each die once.

If the probability of rolling one 3 and one 4 is 1/24, what is the probability of rolling two 1’s?

Answer 1

`(1)/(16)`

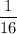
Explanation:

Probability Distribution Table for X

Where X is the score on a fair, six-sided dice:

`\begin{array}c\cline{1-7} x & 1 & 2 & 3 & 4 & 5 & 6\\\cline{1-7} \text{P}(X=x) \phantom{\frac11}&(1)/(6) & (1)/(6) & (1)/(6) & (1)/(6) & (1)/(6) & (1)/(6) \\\cline{1-7}\end{array}`

Probability Distribution Table for Y

Where Y is the score on an unfair, six-sided dice, and the probabilities of rolling numbers 2, 3, 4, 5 and 6 are equal, and the probability of rolling a 1 has a different value:

`\begin{array}c\cline{1-7} y & 1 & 2 & 3 & 4 & 5 & 6\\\cline{1-7} \text{P}(Y=y) \phantom{\frac11}&1-5k&k&k&k&k&k\\\cline{1-7}\end{array}`

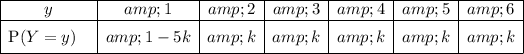
Note: The probabilities of all the possible values that a discrete random variable can take add up to 1.

The outcomes of rolling one 3 and one 4 are:

• Rolling a 3 with the first die and a 4 with the second die, OR
• Rolling a 4 with the first die and a 3 with the second die.

Given the probability of rolling one 3 and one 4 is ¹/₂₄:

`\implies \text{P}(X=3)\; \text{and} \; \text{P}(Y=4) \; \text{or} \; \; \text{P}(X=4) \; \; \text{and} \; \; \text{P}(Y=3)=(1)/(24)`

`\implies (1)/(6) * k +(1)/(6) * k=(1)/(24)`

`\implies (k)/(6) + (k)/(6)=(1)/(24)`

`\implies (2k)/(6)=(1)/(24)`

`\implies 24(2k)=6`

`\implies 48k=6`

`\implies k=(1)/(8)`

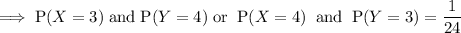
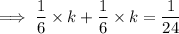
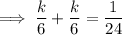
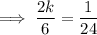
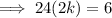
Therefore:

`\implies 1-5k=1-(5)/(8)=(3)/(8)`

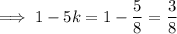
Hence, the probability distribution table for the unfair 6-sided dice is:

`\begin{array}\cline{1-7} y & 1 & 2 & 3 & 4 & 5 & 6\\\cline{1-7} \text{P}(Y=y) \phantom{\frac11}&(3)/(8) & (1)/(8) & (1)/(8)& (1)/(8) & (1)/(8)& (1)/(8) \\\cline{1-7}\end{array}`

There is only one possible outcome of rolling two 1's, so the probability of rolling two 1's is:

`\implies \text{P$(X=1)$ and P$(Y=1)$}=(1)/(6)*(3)/(8)=(3)/(48)=(1)/(16)`

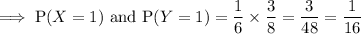
Note: Please see attachment for the sample-space diagram showing the possible outcomes of rolling two dice. The possible outcomes of rolling one 3 and one 4 are highlighted in yellow. The possible outcome of rolling two 1's is highlighted in blue.