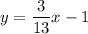Linear Equations
We typically write linear equations in slope-intercept form:

- m = slope
- b = y-intercept (the value of y when x=0)
Solving the Question
We're given:
- Line passes through (0, -1) and ( -13, -4)
1) Determine the slope (m)
To find the slope, we can use the slope equation:
 where
where
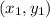 and
and
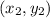 are two points through which the line passes
are two points through which the line passes
⇒ Plug in the given points:
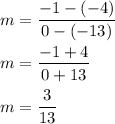
Therefore, the slope of the line is
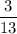 . Plug this into
. Plug this into
 :
:
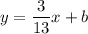
1) Determine the y-intercept (b)
In this case, the y-intercept is already given to us.
The y-intercept is the value of y when x=0. Given that the line passes through (0,-1), we know that this is -1.
Plug this into
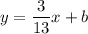 :
:
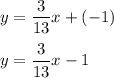
Answer