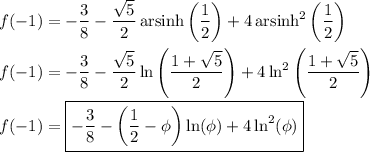Question

`\rm\sum_(n=2)^\infty ((-1)^n)/(n^2(n^2-1)) \binom{2n}{n}^( - 1)\\`


`\:\:\:\:\:\:\:`​

Answer 1

Let

`\displaystyle f(x) = \sum_(n=2)^\infty \frac{x^n}{n^2(n^2-1) \binom{2n}n}`

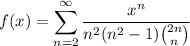
Differentiate and multiply by
`x`.

`\displaystyle xf'(x) = \sum_(n=2)^\infty \frac{x^n}{n(n^2-1) \binom{2n}n}`

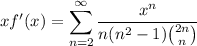
Now differentiate twice.

`\displaystyle x f''(x) + f'(x) = \sum_(n=2)^\infty \frac{x^(n-1)}{(n^2-1)\binom{2n}n}`

`\displaystyle xf'''(x) + 2f''(x) = \sum_(n=2)^\infty \frac{x^(n-2)}{(n+1)\binom{2n}n}`

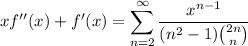
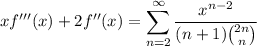
Multiply by
`x^3`.

`\displaystyle x^4 f'''(x) + 2x^3 f''(x) = \sum_(n=2)^\infty \frac{x^(n+1)}{(n+1)\binom{2n}n}`

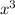Differentiate one last time and multiply by
`\frac1x`.

`\displaystyle x^3 f^((4))(x) + 6x^2 f'''(x) + 6x f''(x) = \sum_(n=2)^\infty \frac{x^(n-1)}{\binom{2n}n}`

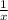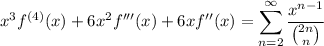
Now integrate with the fundamental theorem of calculus, noting that
`f(0)=f'(0)=0` follows from our series definition. We do this twice and make use of the recurrence

`I_n = \displaystyle \int_0^x y^n f^((n+1))(y) \, dy = x^n f^((n))(x) - n I_(n-1)`

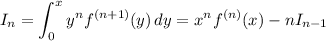
Integrating once yields

`\displaystyle x^3 f'''(x) + 3x^2 f''(x) = \sum_(n=2)^\infty \frac{x^n}{n \binom{2n}n}`

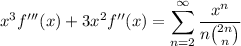
Multiply by
`\frac1x`.

`\displaystyle x^2 f'''(x) + 3x f''(x) = \sum_(n=2)^\infty \frac{x^(n-1)}{n \binom{2n}n}`

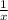Integrating once more yields the ordinary differential equation

`\displaystyle x^2 f''(x) + x f'(x) - f(x) = \sum_(n=2)^\infty \frac{x^n}{n^2 \binom{2n}n}`

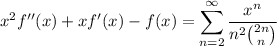
and we recognize the right side as the series

`\displaystyle \sum_(n=2)^\infty \frac{x^n}{n^2 \binom{2n}n} = 2\arcsin^2\left(\frac{\sqrt x}2\right) - \frac x2`

Solving the differential equation is quite doable with the variation of parameters method; we ultimately find

`\displaystyle f(x) = \frac12 + \frac{7x}8 - \left(\frac1x+\frac12\right) \sqrt x √(4-x) \, \arcsin\left(\frac{\sqrt x}2\right) + 2 \left(\frac1x-1\right) \arcsin^2\left(\frac{\sqrt x}2\right)`

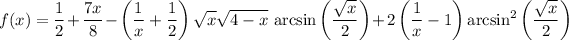
Recover the sum we want by letting
`x=-1`. Recall that

`\arcsin(iz) = i \,\mathrm{arsinh}(z) = i\ln(z + √(1+z^2))`

Then we have the following equivalent results involving our old friend
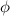`\phi`.

`\displaystyle f(-1) = -\frac38 - \frac{\sqrt5}2\, \mathrm{arsinh}\left(\frac12\right) + 4 \,\mathrm{arsinh}^2\left(\frac12\right) \\\\ f(-1) = -\frac38 - \frac{\sqrt5}2 \ln\left(\frac{1+\sqrt5}2\right) + 4 \ln^2\left(\frac{1+\sqrt5}2\right) \\\\ f(-1) = \boxed{-\frac38 - \left(\frac12 - \phi\right) \ln(\phi) + 4 \ln^2(\phi)}`