Answer:
Proofs provided below
Explanation:
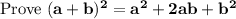
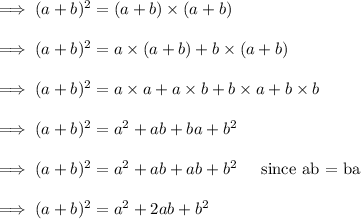
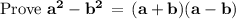
1. Add and subtract ab to LHS
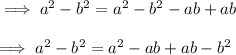
2. Factorize the above expression
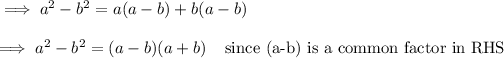
∴ (a² - b²) = (a - b) (a + b)
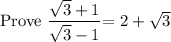
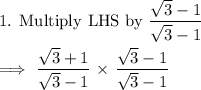
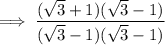
Numerator is
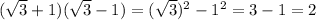
Denominator is
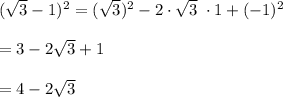
So LHS becomes
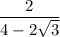
Dividing numerator and denominator by 2 yields
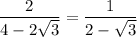
Multiply numerator and denominator by
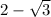
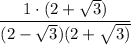
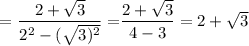
Hence Proved