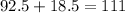Question

Please help, I’ve been trying to do this for a couple of hours now but I can’t seem to figure it out.

The tables show a Linear function that represents your earnings y in dollars after x working hours

(Picture below)

What is the totals earnings for the 6th hour?

$

What is your hourly wage?

$

Answer 1

total earnings at 6th hour: 111

hourly wage (slope): 18.5

Explanation:

A linear function has a linear relationship, which essentially states as x increases by one, the y-value increases by some constant amount yielding a straight line.

The slope, or how much the y-value changes as x changes by 1 is generally written as:
`m=(y_2-y_1)/(x_2-x_1)`

We can choose any two points and this should yield the slope of the function, but it's a lot easier to choose y-values that are only separated by an x-value of one.

Let's say:
`(x_1, y_1)=(4,\ 74)\text{ and }(x_2,y_2)=(5,\ 92.50)`

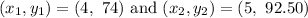
If we plug the values into the slope formula we just get:
`(92.50-74)/(5-4)=(92.50-74)/(1)=92.50-74`

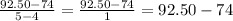
And this makes sense, since by definition of a slope, it's just the change in y over change in x. This is equivalent to how much the y-value changes as x increases by one, so if we select two values with a difference of one in their x-values, the slope just turns out to be the difference between the two numbers.

Simplifying our expression we get:
`92.50-74=18.5`

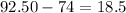
This slope in this context represents how earnings increases as the hour increases, or in other words the hourly wage.

To calculate the earnings of the 6th hour we can just use the definition of a slope. From the x-value 5 to the x-value 6, the y-value should simply increase 18.5

So adding 18.5 to the y-value at x=5 we get:
`92.5+18.5=111`