Question

Find the first derivative.

Answer: y’ = 2/3 x^1/2 - 2/ sqrt of x - 5/2x^2/3

I’m given an answer but don’t know how to get it.

Answer 1

`\quad \huge \quad \quad \boxed{ \tt \:Answer }`

`\qquad\displaystyle \tt \rightarrow \: (dy)/(dx) = \frac{ √(x) (2x - 4) -( \frac{{x}^(2) - 4x + 5) }{2 √(x) } )}{x }`

____________________________________

`\large \tt Solution \: :`

`\qquad\displaystyle \tt \rightarrow \: y = \frac{ {x}^(2) - 4x + 5 }{ √(x) }`

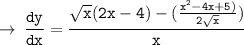
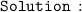
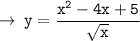
We know, division rule of differentiation :

`\qquad\displaystyle \tt \rightarrow \: y = (u)/(v)`

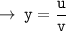
then,

`\qquad\displaystyle \tt \rightarrow \: (dy)/(dx) = \frac{v(du)/(dx) - u (dv)/(dx) }{(v) {}^(2) }`

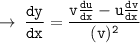
So, let's do the same in given equation :

`\qquad\displaystyle \tt \rightarrow \: (dy)/(dx) = \frac{ √(x) (d)/(dx)(x {}^(2) - 4x + 5) - ( {x}^(2) - 4x + 5) (d)/(dx)( √(x) ) }{( √(x) ) {}^(2) }`

`\qquad\displaystyle \tt \rightarrow \: (dy)/(dx) = \frac{ √(x) (2x - 4) -( {x}^(2) - 4x + 5) (1)/(2 √(x) ) }{x }`

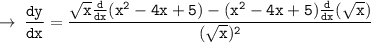
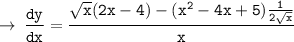
[ This is the required Answer, but you can simplify it however you want according to the choices given ]

`\qquad\displaystyle \tt \rightarrow \: (dy)/(dx) = \frac{x \bigg( (√(x) (2x - 4))/(x) -( {x}^(2) - 4x + 5) (1)/(2x √(x) ) \bigg)}{x }`

`\qquad\displaystyle \tt \rightarrow \: (dy)/(dx) = (√(x) (2x - 4))/(x) -( {x}^(2) - 4x + 5) (1)/(2x √(x) )`

`\qquad\displaystyle \tt \rightarrow \: (dy)/(dx) = ((2x - 4))/( √( x)) - \frac{( {x}^(2) - 4x + 5) }{2 \sqrt{x {}^(3) } }`

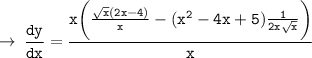
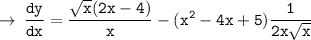
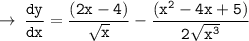
Answered by : ❝ AǫᴜᴀWɪᴢ ❞