Question

Assume that the radius r of a sphere is expanding at a rate of 70 cm/min. The volume of a sphere is V = 3/4pi r^3 and its surface

area is 4pi r². Determine the rate at which the surface area is changing with respect to time when r = 40 cm.
(Use symbolic notation and fractions where needed.)

Answer 1

The rate at which the surface area is changing with respect to time when r = 40 cm is 22400π cm²/min

Not sure if you want it in absolute values since the question says use symbolic notation but if so, multiplying by π gives 70371.675 cm²/min

Explanation:

`\text {Volume of a sphere of radius r is given by }\\\\ \text {$V = (3)/(4)\pi r^3$}`

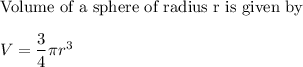
The surface area of a sphere of radius r is given by:

`\\S = 4\pi r^2\\`

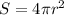
The rate of change of surface area is given by

`(dS)/(dt) = (d)/(dt)\left(4\pi r^2\right)}\\\\(dS)/(dt) = 4 \pi (d)/(dt)\left( r^2\right)}\\\\\\(d)/(dt)(r^2) = 2r(dr)/(dt)\\\\\\`

`(dS)/(dt) = 8\pi r (dr)/(dt)`

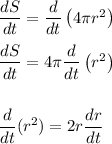
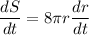
We are given that
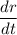`\text{$(dr)/(dt)$}` = 70 cm/min and asked to find rate of change of S when r = 40 cm

Substituting these values into the equation for
`(dS)/(dt)`

`(dS)/(dt) = 8 \pi \cdot 40 \cdot 70\\\\\\\\(dS)/(dt) = 22400 \pi \;cm^2/min`

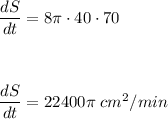
In absolute values