2 Answers

David Boshton · Answer 1 · 2023-03-17T11:13:22+0000

$\quad \huge \quad \quad \boxed{ \tt \:Answer }$

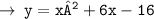
$\qquad \tt \rightarrow \: y = x² +6x -16$

____________________________________

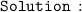
$\large \tt Solution \: :$

The values of x for which the curve cuts/touches the x - axis are roots of that particular polynomial.

So, the values of x, when y = 0 are the roots of the given quadratic function.

that is : x = -8 and x = 2

And it can be represented as :

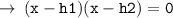
$\qquad \tt \rightarrow \: (x - h1)(x - h2)= 0$

[ h1 and h2 represents roots of the quadratic function ]

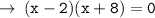
$\qquad \tt \rightarrow \: (x -2)(x + 8) = 0$

It can be further simplified as :

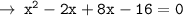
$\qquad \tt \rightarrow \: {x}^(2) -2x +8x -16 = 0$

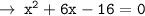
$\qquad \tt \rightarrow \: x {}^(2) +6x -16 = 0$

Answered by : ❝ AǫᴜᴀWɪᴢ ❞

Please log in or register to add a comment.