Question

Module 2 question 6

The cannon on a battleship can fire a shell a maximum distance of 48.0 km.
(a) Calculate the initial velocity of the shell.
m/s

(b) What maximum height does it reach? (At its highest, the shell is above a substantial part of the atmosphere--but air resistance is not really negligible as assumed to make this problem easier.)
m

(c) The ocean is not flat, since the earth is curved. How many meters lower will its surface be 48.0 km from the ship along a horizontal line parallel to the surface at the ship?
mDoes your answer imply that error introduced by the assumption of a flat earth in projectile motion is significant here? (Select all that apply.)
The error is significant compared to the distance of travel.
The error is insignificant compared to the distance of travel.
The error is insignificant compared to the size of a target.
The error could be significant compared to the size of a target.

Answer 1

1. The initial velocity of the shell = 685.86 m / s
2. The maximum height reached by the shell = 12098.15 m
3. It will be 180 meters lower, 48 km from the ship.

( a ) R = u² sin 2θ / g

θ = 45°

R = 48 km = 48000 m

g = 9.8 m / s²

u² = ( 48000 * 9.8 ) / sin 2 ( 45 )

u² = 470400 / 1

u = 685.86 m / s

( b ) H = u² sin²θ / 2g

H = 685.85² sin²45 / 2 * 9.8

H = 12098.15 m

( c ) The radius of Earth, the horizontal distance travelled by the shell and the distance from final position of cannon and center of Earth makes a right angled triangle.

According to Pythagoras theorem,

x² = 48² + ( 6.371 * 10³)²

x² = 2304 + ( 40.589641 *
`10^(6)` )

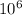x² = ( 23.04 * 10² ) + ( 405896.41 * 10² )

x² = 405919.45 * 10²

x = 6371.18

At 48 km from the ship, the distance lower form the surface the shell lands is,

d = 6371.18 - 6371

d = 0.18 km

Compared to the distance travelled of 48 km, the error of 0.18 km is insignificant

Therefore,

1. The initial velocity of the shell = 685.86 m / s
2. The maximum height reached by the shell = 12098.15 m
3. It will be 180 meters lower, 48 km from the ship.