Answer:
x = 7
Explanation:
Vertical Angle Theorem
When two straight lines intersect, they form two pairs of angles. The vertically opposite (non-adjacent) angles are congruent.
Angles on a Straight Line Theorem
The sum of angles formed on a straight line is equal to 180°.
The error made is confusing the Vertical Angle Theorem with the Angles on a Straight Line Theorem. To find x, we should either:
- Equal a pair of vertical angles and solve for x, or
- Equal the sum a pair of angles that form a straight line to 180° and solve for x.
Applying the Vertical Angle Theorem:

Applying the Angles on a Straight Line Theorem:
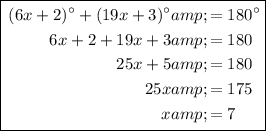
Therefore, the value of x is
 .
.