Answer: (0,-2)
Explanation:
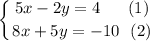
Multiply equation (1) by 5, and equation (2) by 2:
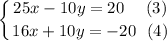
Add equations (3) and (4):
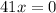
Divide both parts of the equation by 41:
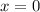
Let's substitute the value of x into equation (2):
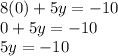
Divide both parts of the equation by 5:
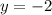
Thus, (0,-2)