Question

Solve the quadratic equations by factoring.

1. 5x^2 = 3x + 2

2. x^2 - 4x + 3 = 0

Help on these two problems above would be very appreciated, thanks!

Answer 1

Solving by factoring in steps shown below

Question 1

• 5x² = 3x + 2
• 5x² - 3x - 2 = 0
• 5x² - 5x + 2x - 2 = 0
• 5x(x - 1) + 2(x - 1) = 0
• (5x + 2)(x - 1) = 0

• 5x + 2 = 0 and x - 1 = 0
• 5x = - 2 and x = 1
• x = - 2/5 and x = 1

Question 2

• x² - 4x + 3 = 0
• x² - x - 3x + 3 = 0
• x(x - 1) - 3(x - 1) = 0
• (x - 3)(x - 1) = 0

• x - 3 = 0 and x - 1 = 0
• x = 3 and x = 1

Answer 2

`\textsf{1. \quad $x=1, \quad x=-(2)/(5)$}`

`\textsf{2. \quad $x=1, \quad x=3$}`

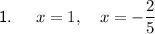
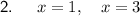
Explanation:

Solving quadratic equations by factoring

• To factor a quadratic in the form
  `ax^2+bx+c` , find two numbers that multiply to
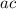  `ac` and sum to
  `b`, and rewrite
  `b` as the sum of these two numbers.
• Factor the first two terms and the last two terms separately.
• Factor out the common term.
• Solve for x by applying the zero-product property.

Question 1

Given equation:

`5x^2=3x+2`

Subtract (3x + 2) from both sides:

`\implies 5x^2-(3x+2)=3x+2-(3x+2)`

`\implies 5x^2-3x-2=0`

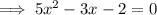
Find two numbers that multiply to
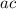`ac` and sum to
`b`, and rewrite
`b` as the sum of these two numbers:

`\implies ac=5 \cdot -2=-10`

`\implies b=-3`

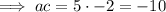
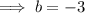
Therefore, the two numbers are -5 and 2.

Rewrite
`b` as the sum of the two numbers:

`\implies 5x^2-5x+2x-2=0`

Factor the first two terms and the last two terms separately:

`\implies 5x(x-1)+2(x-1)=0`

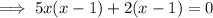
Factor out the common term (x - 1):

`\implies (5x+2)(x-1)=0`

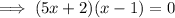
Apply the zero-product property:

`\implies 5x+2=0 \implies x=-(2)/(5)`

`\implies x-1=0 \implies x=1`

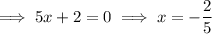
Therefore, the solutions are:

`\boxed{x=1, \quad x=-(2)/(5)}`

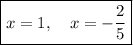
Question 2

Given equation:

`\implies x^2-4x+3=0`

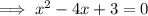
Find two numbers that multiply to
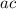`ac` and sum to
`b`, and rewrite
`b` as the sum of these two numbers:

`\implies ac=1 \cdot 3=3`

`\implies b=-4`

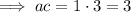
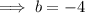
Therefore, the two numbers are -3 and -1.

Rewrite
`b` as the sum of the two numbers:

`\implies x^2-3x-x+3=0`

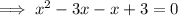
Factor the first two terms and the last two terms separately:

`\implies x(x-3)-1(x-3)=0`

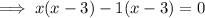
Factor out the common term (x - 3):

`\implies (x-1)(x-3)=0`

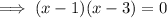
Apply the zero-product property:

`\implies x-1=0 \implies x=1`

`\implies x-3=0 \implies x=3`

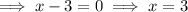
Therefore, the solutions are:

`\boxed{x=1, \quad x=3}`