Question

Identify the interval on which the quadratic function is positive.

1. y = -7x^2 + 35x - 28

Identify the interval on which the quadratic function is negative.

2. y = 2x^2 - 4x - 16

Help on these problems above would be appreciated, thanks! (ɔ◔‿◔)ɔ ♥

Answer 1

`\textsf{1. \quad Solution: $1 < x < 4$,\quad Interval notation: $(1, 4)$}`

`\textsf{2. \quad Solution: $-2 < x < 4$,\quad Interval notation: $(-2, 4)$}`

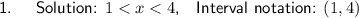
Explanation:

Question 1

The intervals on which a quadratic function is positive are those intervals where the function is above the x-axis, i.e. where y > 0.

The zeros of the quadratic function are the points at which the parabola crosses the x-axis.

As the given quadratic function has a negative leading coefficient, the parabola opens downwards. Therefore, the interval on which y > 0 is between the zeros.

To find the zeros of the given quadratic function, substitute y = 0 and factor:

`\begin{aligned}y&= 0\\\implies -7x^2+35x-28& = 0\\-7(x^2-5x+4)& = 0\\x^2-5x+4& = 0\\x^2-x-4x+4& = 0\\x(x-1)-4(x-1)&= 0\\(x-1)(x-4)& = 0\end{aligned}`

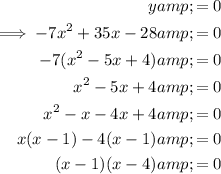
Apply the zero-product property:

`\implies x-1=0 \implies x=1`

`\implies x-4=0 \implies x=4`

Therefore, the interval on which the function is positive is:

• Solution: 1 < x < 4
• Interval notation: (1, 4)

Question 2

The intervals on which a quadratic function is negative are those intervals where the function is below the x-axis, i.e. where y < 0.

The zeros of the quadratic function are the points at which the parabola crosses the x-axis.

As the given quadratic function has a positive leading coefficient, the parabola opens upwards. Therefore, the interval on which y < 0 is between the zeros.

To find the zeros of the given quadratic function, substitute y = 0 and factor:

`\begin{aligned}y&= 0\\\implies 2x^2-4x-16& = 0\\2(x^2-2x-8)& = 0\\x^2-2x-8& = 0\\x^2-4x+2-8& = 0\\x(x-4)+2(x-4)&= 0\\(x+2)(x-4)& = 0\end{aligned}`

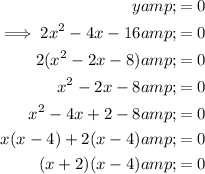
Apply the zero-product property:

`\implies x+2=0 \implies x=-2`

`\implies x-4=0 \implies x=4`

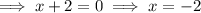
Therefore, the interval on which the function is negative is:

• Solution: -2 < x < 4
• Interval notation: (-2, 4)