Question

Identify the interval(s) on which each quadratic function is positive.

1. y= x^2 + 2x - 8

2. y= -x^2 +4x +12

3. y= 5x^2 - 3x - 8

Help on these three problems above would be greatly appreciated, thanks! ☜(ˆ▿ˆc)

Answer 1

`\textsf{1. \quad $x < -4$ or $x > 2$}`

`\textsf{2. \quad $-2 < x < 6$}`

`\textsf{3. \quad $x < -1$ or $x > \frac{8}[5}$}`
`\textsf{3. \quad $x < -1$ or $x > \frac{8}[5}$}`
`\textsf{3. \quad $x < -1$ or $x > (8)/(5)$}`

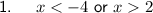
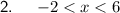
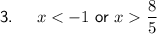
Explanation:

The intervals on which a quadratic function is positive are those intervals where the function is above the x-axis, i.e. where y > 0.

The zeros of the quadratic function are the points at which the parabola crosses the x-axis.

If the leading coefficient of a quadratic function is positive, the parabola opens upwards.

If the leading coefficient of a quadratic function is negative, the parabola opens downwards.

Therefore, to find the intervals on which each quadratic function is positive:

• Calculate the zeros.
• Determine if the parabola opens upwards or downwards.
• If the parabola opens upwards, the intervals are less than the smaller zero and greater than the larger zero.
• If the parabola opens downwards, the interval is between the zeros.

Question 1

Given function:

`y=x^2+2x-8`

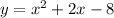
Factor the given function:

`\implies y= x^2+4x-2x-8`

`\implies y=x(x+4)-2(x+4)`

`\implies y=(x-2)(x+4)`

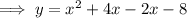
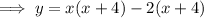
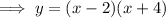
Substitute y = 0 to find the zeros:

`\implies (x-2)(x+4)=0`

`\implies x-2=0 \implies x=2`

`\implies x+4=0 \implies x=-4`

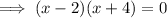
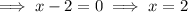
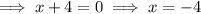
The leading coefficient is positive, so the parabola opens upwards.

Therefore, the interval on which the function is positive is:

• Solution: x < -4 or x > 2
• Interval notation: (-∞, -4) ∪ (2, ∞)

Question 2

Given function:

`y=-x^2+4x+12`

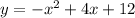
Factor the given function:

`\implies y=-(x^2-4x-12)`

`\implies y=-(x^2-6x+2x-12)`

`\implies y=-(x(x-6)+2(x-6))`

`\implies y=-(x+2)(x-6)`

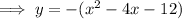
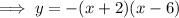
Substitute y = 0 to find the zeros:

`\implies -(x+2)(x-6)=0`

`\implies (x+2)(x-6)=0`

`\implies x+2=0 \implies x=-2`

`\implies x-6=0 \implies x=6`

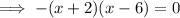
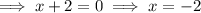
The leading coefficient is negative, so the parabola opens downwards.

Therefore, the interval on which the function is positive is:

• Solution: -2 < x < 6
• Interval notation: (-2, 6)

Question 3

Given function:

`y=5x^2-3x-8`

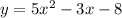
Factor the given function:

`\implies y=5x^2-8x+5x-8`

`\implies y=x(5x-8)+1(5x-8)`

`\implies y=(x+1)(5x-8)`

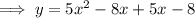
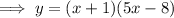
Substitute y = 0 to find the zeros:

`\implies (x+1)(5x-8)=0`

`\implies x+1=0 \implies x=-1`

`\implies 5x-8=0 \implies x=(8)/(5)`

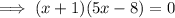
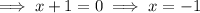
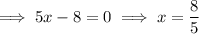
The leading coefficient is positive, so the parabola opens upwards.

Therefore, the interval on which the function is positive is:

• Solution: x < -1 or x > ⁸/₅
• Interval notation: (-∞, -1) ∪ (⁸/₅, ∞)