Question

A penny is dropped from the top of a new building. Its height in feet can be modeled by the equation y = 256 - 16^{2} , where x is the time in seconds since the penny was dropped. How long does it take for the penny to reach the ground?

I would greatly appreciate help with this word problem, thanks!

≧◠ᴥ◠≦✊

Answer 1

4 seconds

Explanation:

Given equation:

`y=256-16x^2`

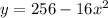
where:

• y = The height of the penny (in feet).
• x = The time since the penny was dropped (in seconds).

The penny reaches the ground when the height is zero, so when y = 0.

Substitute y = 0 into the given equation and solve for x:

`\begin{aligned}y&=256-16x^2\\y=0 \implies 0&=256-16x^2\\0+16x^2&=256-16x^2+16x^2\\16x^2&=256\\(16x^2)/(16)&=(256)/(16)\\x^2&=16\\√(x^2)&=√(16)\\x&=\pm4\end{aligned}`

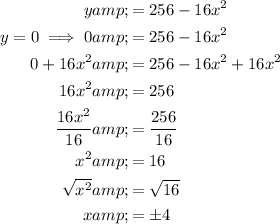
As time is positive, x = 4 only.

Therefore, it takes 4 seconds for the penny to reach the ground.