
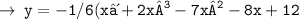
____________________________________
The values of x for which curves cuts/touches the x - axis are the roots of that particular polynomial.
And that polynomial can be depicted in form :
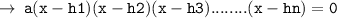
[ where, h1, h2, h3... hn represents roots of that polynomial, and " a " is the stretch of curve]
And by that, we can sort out the roots of given polynomial that are :
Since there are four roots, the least degree polynomial formed will have bi - quadratic polynomial.
And it will be represented as :
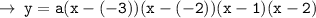
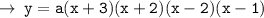
And it can be further solved to get ~
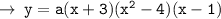
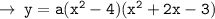
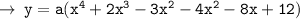
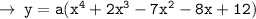
Now, it's time to evaluate the value of a, for that we can just use a point that satifys the curve ( i.e (0 , -2)
plug in the values :
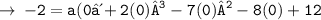
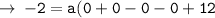
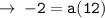

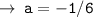
Therefore, the required equation is :
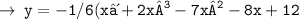
Answered by : ❝ AǫᴜᴀWɪᴢ ❞