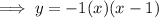Question

Write an equation for a parabola with x-intercepts at 0 and 1 and which passes through the point (2, -2).

I would greatly appreciate some help with this!

（っ＾▿＾）

Answer 1

`y=-x^2+x`

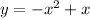
Explanation:

Intercept form of a quadratic equation:

`y=a(x-p)(x-q)`

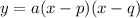
where:

• p and q are the x-intercepts.
• a is some constant.

Given:

• x-intercepts: 0 and 1
• Point on the curve: (2, -2)

Substitute the given values into the formula and solve for a:

`\begin{aligned}y&=a(x-p)(x-q)\\\\\implies -2&=a(2-0)(2-1)\\-2&=a(2)(1)\\-2&=2a\\(2a)/(2)&=(-2)/(2)\\\implies a&=-1\end{aligned}`

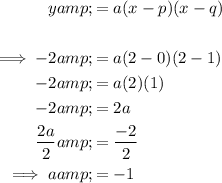
Substitute the given x-intercepts and the found value of a into the formula:

`y=-1(x-0)(x-1)`

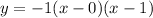
Expand to standard form:

`\implies y=-1(x)(x-1)`

`\implies y=-x(x-1)`

`\implies y=-x^2+x`

Answer 2

y = -x(x - 1).

Explanation:

y = a(x - b)(x - c) where a is a constant and b and c are the x-intercepts.

y = a(x - 0)( x - 1)

y = ax(x - 1).

When x = 2, y = -2 so:

-2 = a(2) (2 - 1)

2a = -2

a = -1.

So the equation is y = -x(x - 1).