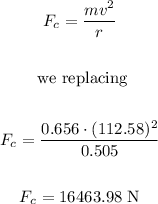ANSWER:
(a) 112.58 m/s
(b) 16463.98 N
Explanation:
Given:
Frequency (F) = 35.5 Hz
Mass (m) = 0.656 kg
Radius (r) = 50.5 cm = 0.505 m
(a) To determine the speed with which the mass moves, we must first calculate the angular speed, like this:
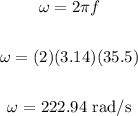
Now we can calculate the speed, with the help of the radius:
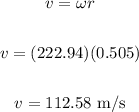
(b) The centripetal force is calculated using the following formula: