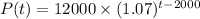iven:
heere are given that the population in the year 2000 was 12000 and the growth rate is 7% per year.
xplanation:
ccording to the question:
For t =0 which is the year 2000:
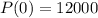
For t = 1:
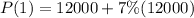
If we say r is the rate, then:
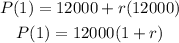
Then,
For t = 2:
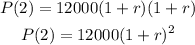
And,
For t = 3:
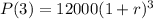
Therefore our function should be:
(a):
he population function:
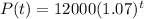
Now,
(b):
ccording to the question:
2008 is 8 year from year 2000:
Therefore, t = 8:
Then,
Put the value 8 for t into the function (a):
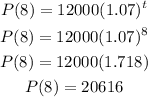
inal answer: