ANSWER
x = 4 or x = -9
Explanation:
As you can see from the question provided, you were given the following logarithms equation
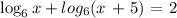
Recall that,
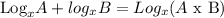

The next thing is to replace the values and simplify
![\begin{gathered} \log _6x(x\text{ + 5) = 2} \\ x(x+5)=6^2 \\ \text{Open the parenthesis} \\ x^2\text{ + 5x = 36} \\ x^2\text{ + 5x - 36 = 0} \end{gathered}]()
As you can see from the last process, the logarithms function resulted in a quadratic equation.
The next thing is to solve the equation using the factorization method.
Note that, the general quadratic function is given below as
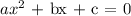
Relating the two equations, you will have the following data
• a = 1
,
• b = 5
,
• c = -36
The next thing is to find the value of ac
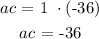
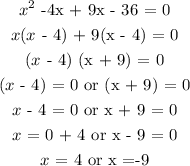
Hence, the values of x are 4 and -9