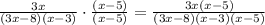Question

Rewrite as equivalent rational expressions with denominator (3x-8)(x-5)(x-3)

Answer 1

we have the expression

`(4)/(3x^2-23x+40)`

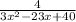
Rewrite as equivalent rational expressions with denominator (3x-8)(x-5)(x-3)

In this problem

3x^2-23x+40=3(x-5)(3x-8)

so

`(4)/(3x^2-23x+40)=(4)/(3\mleft(x-5\mright)\mleft(3x-8\mright))`

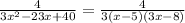
Multiply by (x-3)/(x-3)

`(4)/(3(x-5)(3x-8))\cdot((x-3))/((x-3))=(4(x-3))/(3(x-5)(3x-8)(x-3))`

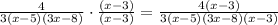
Part 2

we have the expression

`(9x)/(3x^2-17x+24)`

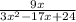
we have that

3x^2-17x+24=3(3x-8)(x-3)

so

`(9x)/(3x^2-17x+24)=(9x)/(3\mleft(3x-8\mright)\mleft(x-3\mright))=(3x)/((3x-8)(x-3))`

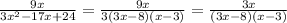
Multiply the expression by (x-5)/(x-5)

`(3x)/((3x-8)(x-3))\cdot((x-5))/((x-5))=(3x(x-5))/((3x-8)(x-3)(x-5))`