1 Answer

Keysersoze · Answer 1 · 2023-09-30T05:11:23+0000

In order to find the time it takes, first let's convert the distance from miles per hour to feet per second: calculate the acceleration using Torricelli's equation

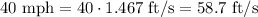
$40\text{ mph}=40\cdot1.467\text{ ft/s}=58.7\text{ ft/s}$

Then, let's :

$\begin{gathered} V^2=V_0^2+2\cdot a\cdot d\\ \\ 0^2=58.7^2+2\cdot a\cdot50\\ \\ 100a=-3445.7\\ \\ a=-34.46\text{ ft/s^^b2} \end{gathered}$

Now, we calculate the time with the formula below:

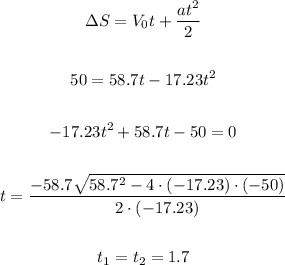
$\begin{gathered} \Delta S=V_0t+(at^2)/(2)\\ \\ 50=58.7t-17.23t^2\\ \\ -17.23t^2+58.7t-50=0\\ \\ t=(-58.7√(58.7^2-4\cdot(-17.23)\cdot(-50)))/(2\cdot(-17.23))\\ \\ t_1=t_2=1.7 \end{gathered}$

Therefore the time required is 1.7 seconds.

0 Comments

Please log in or register to add a comment.

Please log in or register to answer this question.

1 Answer

0 Comments

Please log in or register to add a comment.

Other Questions