Question

Hello, i need help with this question

Answer 1

The area of ​​a triangle is given by the formula:

`\begin{gathered} A=(b\cdot h)/(2) \\ \text{ Where b is the base and} \\ h\text{ is the height of the triangle} \end{gathered}`

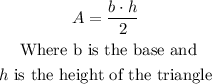
From the information given you know that the measure of the height of the triangle EFG is 16 cm but the measure of the base of the triangle is unknown.

To find the measure of the base, you can first find the measure of the middle of the segment EG using the Pythagorean theorem, since the triangle formed by the vertices F, G, and EG/2 form a right triangle. Graphically,

The formula of the Pythagorean Theorem is

`\begin{gathered} a^2+b^2=c^2 \\ \text{ Where c is the hypotenuse and} \\ a,b\text{ are the sides of the triangle} \end{gathered}`

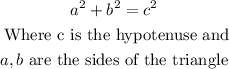
So, you have

`\begin{gathered} a=16 \\ b=(EG)/(2) \\ c=20 \\ (16)^2+b^2=(20)^2 \\ 256+b^2=400 \\ \text{ Subtract 256 from both sides of the equation} \\ 256+b^2-256=400-256 \\ b^2=400-256 \\ b^2=144 \\ \text{ Apply square root to both sides of the equation} \\ \sqrt[]{b^2}=\sqrt[]{144} \\ b=12 \\ \text{ Then} \\ (EG)/(2)=12 \end{gathered}`

Then, the measure of the segment EG, that is, the measure of the base of the triangle EFG is

`\begin{gathered} (EG)/(2)=12 \\ \text{ Multiply by 2 on both sides of the equation} \\ (EG)/(2)\cdot2=12\cdot2 \\ EG=24 \end{gathered}`

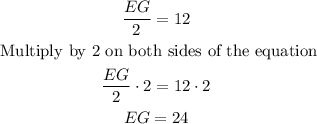
Finally, the area of triangle EFG will be

Therefore, the area of the triangle EFG is 192 square centimeters.