Question

Brian is working his way through school. He works two part-time jobs for a total of 22 hours a week. Job A pays $6.10 per hour, and Job B pays $7.30 per hour. How many hours did he work at each job the week that he made $148.60.

Answer 1

Let a be the number of hours that Brian works at Job A in one week and b be the number of hours that he works at Job B .in one week

Since Brian worked 22 hours per week and he made $148.60, we can set the following system of equations:

`\begin{gathered} a+b=22, \\ 6.10a+7.30b=148.60. \end{gathered}`

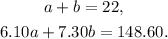
Subtracting b from the first equation we get:

`\begin{gathered} a+b-b=22-b, \\ a=22-b\text{.} \end{gathered}`

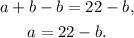
Substituting the above equation in the second one we get:

`6.10(22-b)+7.30b=148.60.`

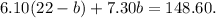
Applying the distributive property we get:

`\begin{gathered} 6.10*22-6.10* b+7.30b=148.60, \\ 134.20+1.20b=148.60. \end{gathered}`

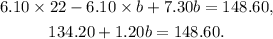
Subtracting 134.20 from the above equation we get:

`\begin{gathered} 134.20+1.20b-134.20=148.60-134.20, \\ 1.20b=14.40. \end{gathered}`

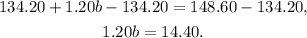
Dividing the above equation by 1.20 we get:

`\begin{gathered} (1.20b)/(1.20)=(14.40)/(1.20), \\ b=12. \end{gathered}`

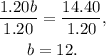
Substituting b=12 in a=22-b we get:

`a=22-12=10.`

Answer: