The parent function given is
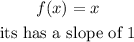
The transformed function given is
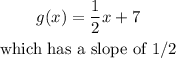
There is a reduction in the slope of the functions which makes the transformed function become less steep
The slope reduced from
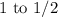
There is also a change in the intercept from

And this indicates that the transformed function has been shifted up by 7 units
With the explanation above, we can therefore conclude that the statement which compares the two graphs of the function is
The graph of g(x) is less steep than the graph of f(x) and the intercept has been shifted up
Hence, The correct answer is OPTION C