To get the percentile
Step 1: Write the formula
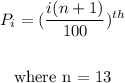
For the 38th percentile
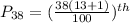
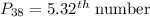
This means that the 38th percentile is between the 5th and 6th number
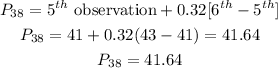
P38 = 41.64This means that approximately 38% of the data lie below 43, when the data are ranked
For the 60th percentile,
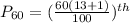
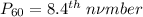
6089
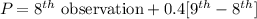
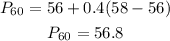
60