Question

Pls help me with my question

Answer 1

Given the figure of an object consists of a cylinder and a rectangular prism.

We will find the volume of the cylinder using the following formula:

`V=\pi r^2h`

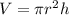
As shown, the diameter of the base = d = 3 ft

So, the radius = r = d/2 = 3/2 = 1.5 ft

And the height = h = 4 ft

Use π = 3

so, the volume of the cylinder will be as follows:

`V=3*1.5^2*4=27\text{ }ft^3`

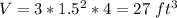
Now, we will find the volume of the rectangular prism using the following formula:

`V=l*w*h`

As shown, the length = l = 7 ft

The width = w = 4 ft

The height = h = 4 ft

So, the volume of the rectangular prism will be as follows:

`V=7*4*4=112\text{ }ft^3`

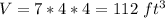
So, the total volume of the object will be =

`27+112=139\text{ }ft^3`

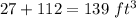
So, the answer will be V = 139 ft³