Given:
A table with the given values of the function y=g(x).
To find the function that represents g(x), we substitute a value of x into the given options.
For:
g(x =3+2x:,:
Let x=3
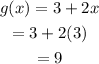
Based on the given table, the value g(x) is 24 when x=3. So g(x)=3+2x is not the function that represents g(x).
For
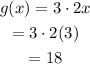
The value of g(x) =18 when x=3, so this is not the function.
For g(x)=3x^2:
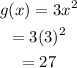
Hence, this is not the function as well.
For g(x)=3(2)^x:
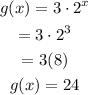
We can notice that when x=3, the value of g(x) =24 which is the same as the value of g(x) in the given table.
To double check this, we plug in the other values of x.
Therefore, the answer is:
