Question

-4x^2-5x=-9 please show a step by step answer

Answer 1

We can solve the quadratic equation using factorization method.

First, let's re-write the equation:

`\begin{gathered} -4x^2\text{ - 5x = -9} \\ \text{divide through by -1 } \\ 4x^2\text{ + 5x = 9} \\ Re-\text{arranging, we have} \\ 4x^2\text{ + 5x - 9 = 0} \end{gathered}`

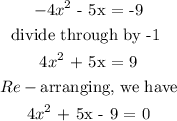
Next, we try to factorize the expression by the left:

`\begin{gathered} 4x^2\text{ - 4x + 9x - 9 = 0} \\ (4x^2\text{ - 4x) + (9x - 9) = 0} \\ 4x\text{ (x - 1) + 9(x -1)}=0 \\ (4x\text{ + 9)(x - 1)}=0 \end{gathered}`

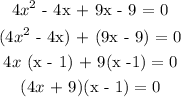
Next, we equate each factor to zero to find the value of x

`\begin{gathered} 4x\text{ + 9 = 0} \\ 4x\text{ = -9} \\ \text{x = }(-9)/(4) \\ x\text{ - 1 = 0} \\ x\text{ = 1} \end{gathered}`

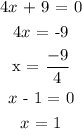
We can conclude that :

`x\text{ = 1 or }(-9)/(4)`

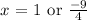
We can also do a check by substituting the value of x back into the equation: