we have the equation
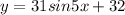
Find out the first derivative
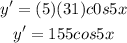
equate to zero the derivative, to find out the critical points
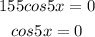
The value of cosine is zero when the angle is 90, 270 degrees (pi/2 and 3pi/2)
so
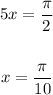
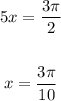
For x=pi/10
Find out the y-coordinate
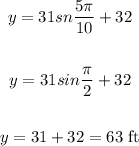
Verify for x=3pi/10
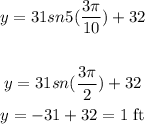
The maximum height is 63 ft