Solution:
The equation of the ellipse in the question is given as
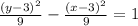
Concept:
The general formula of a hyperbola is
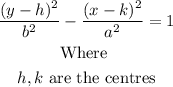
From the above equation by comparing coeficient, we will have
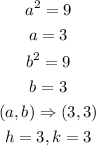
The linear eccentricity c, will be
![\begin{gathered} c=\sqrt[]{a^2+b^2} \\ c=\sqrt[]{3^2+3^2} \\ c=\sqrt[]{9+9} \\ c=\sqrt[]{18} \\ c=3\sqrt[]{2} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/1luh5gf2w4vip3manebh4yrep4sfoo45hu.png)
The vertices of the hyperbola will be calculate using the formula below
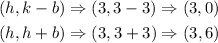
The co-vertex are calculated using the formula below
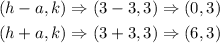
The foci of the hyperbola will be calculated using the formula below
![\begin{gathered} \mleft(h,k-c\mright)\Rightarrow(3,3-3\sqrt[]{2)} \\ \mleft(h,k+c\mright)\Rightarrow\Rightarrow\Rightarrow\mleft(3,3+3\sqrt[]{2}\mright) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/yvij52k0co8ns30tjoamdspr3jata9gu57.png)
The eccentricity, e is
![e=(c)/(b)=\frac{3\sqrt[]{2}}{3}=\sqrt[]{2}](https://img.qammunity.org/2023/formulas/mathematics/high-school/hiczxqtdjokknbjiuooa74jyil20i09aol.png)
Hence,
The sketch of the graph is given below as
The foci is represented with the two red dots on the graph
The vertices are represented above by the two coordinates