The derivate of a function f(x) is determinated as:
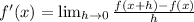
For the function
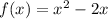
First we have to determine de f ( x + h ) as follow:
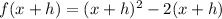
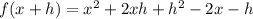
Then we calculate and simplify the coeficient in the first formula
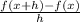
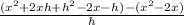
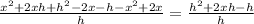
 So the derivate is:
So the derivate is: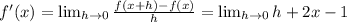
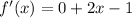
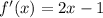
------------------------------------------------------------------------------------The equation of the tangent:
First you need to know that the derivate of a function is equal to the slope (m) of the tangent of this function
And the equation to thist tangent in a specific point will be find using the next formula:
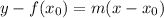
We have to calculate the slope in the point x =4 using the derivate:
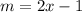
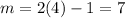
In the point x=4
Calculate the value of f(x0) substituting in the function the given point x:
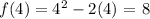
Knowing that we put the value of m and f(x0) in the equation of the tangent:
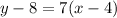


So the equation of the tangent in x= 4 is:
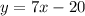
---------------------------------------------------------------------------
The normal line
The slope of the normal line is the opposite of the slope of theu tangent in an espesific point:
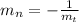
So in this situation is:

The equation of the normal line is given by the next formula:
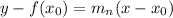
Replacing the data we obtain:
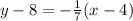

So the equation of the normal line is:
