Hello!
We have the function below:
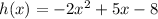
The first step is to identify the coefficients a, b and c:
• a = -2
,
• b = 5
,
• c = -8
Just by analyzing these coefficients, we can say that the concavity of the parabola will be facing downwards because the coefficient a is negative
1st step: using the quadratic formula, we will find the interceptions in the x-axis. Look:
![x=\frac{-b\pm\sqrt[]{b^2-4\cdot a\cdot c}}{2\cdot a}](https://img.qammunity.org/2023/formulas/mathematics/college/uqsn52onz34wdlqp5q7o3d75junrk7u3bj.png)
As we know the coefficients, let's replace them in the formula:
![\begin{gathered} x=\frac{-5\pm\sqrt[]{5^2-4\cdot(-2)\cdot(-8)}}{2\cdot(-2)} \\ \\ x=\frac{-5\pm\sqrt[]{25^{}-64}}{-4}=\frac{-5\pm\sqrt[]{-39}}{-4}= \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/44pcl41ni5ynw8p799sny6ib2fpswv6xqy.png)
Obs: as we obtained a negative square root, we can stop this step here. It means that
2nd step: let's identify the maximum point of it:
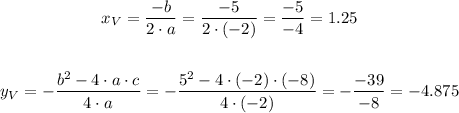
So, the vertex is at the point (x, y) = (1.25, -4.875).
The axis of symmetry is x = 5/4 or also x = 1.25.
Look at the graph below:
Note: if you solve this function when x = 0, you will obtain one interception in the y-axis, look:

So, the y-intercept is at (x, y) = (0, -8) as you can see at the graph.